Conjuntos en Python – set
Los conjuntos son uno de los tipos básicos que provee Python y bastante utilizados. Representan un objeto capaz de almacenar elementos únicos, que además están indexados, por lo que son de gran utilidad para buscar elementos.
Contenido
¿Qué es un conjunto en Python?
Los conjuntos son utilizados en álgebra de conjuntos para hacer operaciones sobre grupos de valores, además de ser utilizados en muchos ámbitos del cálculo.
En Python los conjuntos pueden almacenar valores numéricos o de cualquier tipo, siempre y cuando los valores sean “hasheables”. Los conjuntos son tipos mutables, se garantiza que todos sus elementos son únicos, pero no se garantiza que estén ordenados.
Por lo tanto, algunos ejemplos de tipos hasheables son: los enteros, las cadenas de caracteres, o las tuplas. Sin embargo, las listas no son hasheables, por tanto un conjunto no puede contener listas, pero sí cadenas de caracteres o números.
Ejemplo de conjuntos
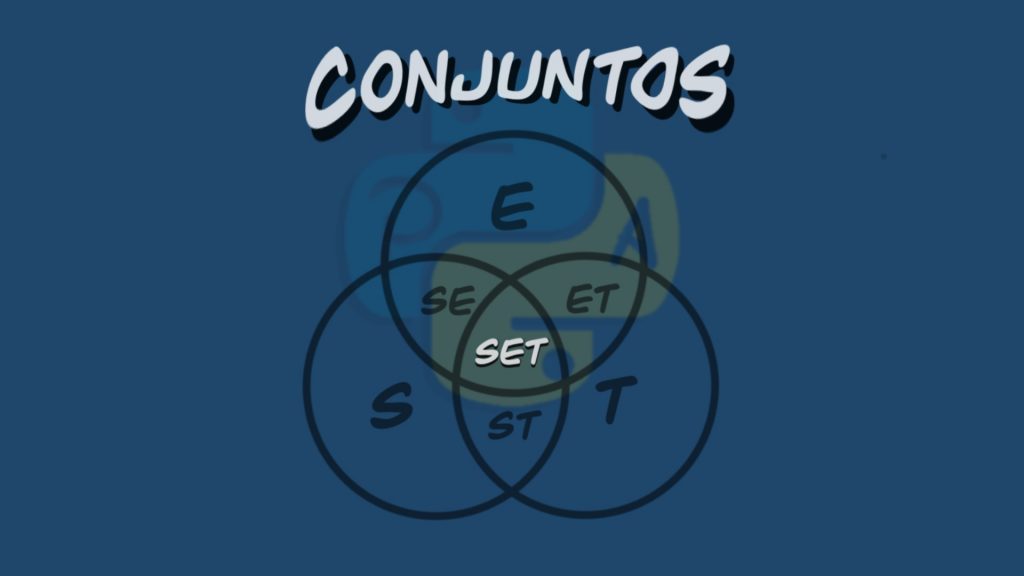
Se utilizará el siguiente ejemplo para mostrar operaciones con conjuntos. Hay un grupo de personas (estudiantes) que están en tres grupos A, B y C. Algunos estudiantes están en varios grupos.
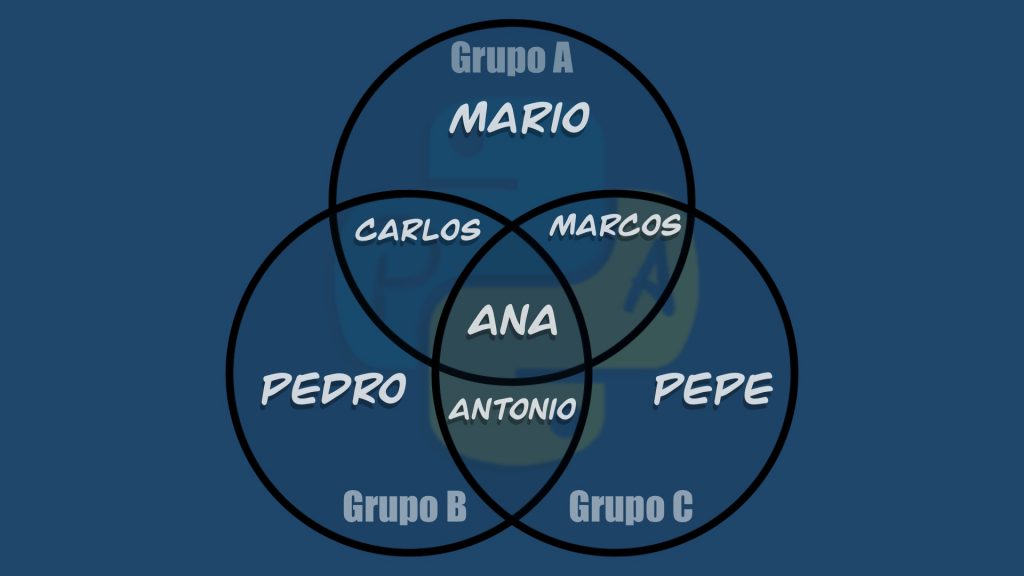
- Primer grupo – Grupo A: Ana, Marcos, Carlos, Mario.
- Segundo grupo – Grupo B: Ana, Pedro, Carlos, Antonio.
- Tercer Grupo – Grupo C: Ana, Antonio, Marcos, Pepe.
La representación gráfica de estos conjuntos sería:
Crear conjuntos en Python
La forma de crear un conjunto es usando el constructor de listas set o como literal usando {<argumentos>}. A continuación se pueden ver ejemplos.
>>> group_a = set(['Ana', 'Marcos', 'Carlos', 'Mario'])
>>> group_b = {'Ana', 'Pedro', 'Carlos', 'Antonio'}
>>> group_c = {'Ana', 'Antonio', 'Marcos', 'Pepe'}
>>> all_students = group_a.union(group_b).union(group_c)
>>> all_students
{'Marcos', 'Carlos', 'Mario', 'Pepe', 'Antonio', 'Pedro', 'Ana'}
>>> a_and_b = group_a.intersection(group_b)
>>> a_and_b
{'Ana', 'Carlos'}
>>> a_and_c = group_a.intersection(group_c)
>>> a_and_c
{'Ana', 'Marcos'}
>>> b_and_c = group_b.intersection(group_c)
>>> b_and_c
{'Ana', 'Antonio'}
>>> common_all = group_a.intersection(group_b).intersection(group_c)
>>> common_all
{'Ana'}Se pueden realizar operaciones interesantes como saber el grupo al que pertenece cada estudiante de forma simple.
>>> group_a = {'Ana', 'Marcos', 'Carlos', 'Mario'}
>>> group_b = {'Ana', 'Pedro', 'Carlos', 'Antonio'}
>>> group_c = {'Ana', 'Antonio', 'Marcos', 'Pepe'}
>>> all_students = group_a.union(group_b).union(group_c)
>>> for student in all_students:
... groups_in = []
... for letter, group in zip('ABC', [group_a, group_b, group_c]):
... if student in group:
... groups_in.append(letter)
... groups_str = '-'.join(groups_in)
... plural = 's' if len(groups_in) > 1 else ''
... print(f'{student} en grupo{plural}: {groups_str}')
...
Ana en grupos: A-B-C
Antonio en grupos: B-C
Pedro en grupo: B
Pepe en grupo: C
Carlos en grupos: A-B
Marcos en grupos: A-C
Mario en grupo: AMétodos disponibles sobre set
A continuación se muestran los métodos disponibles para conjuntos:
>>> dir(set)
['__and__', '__class__', '__contains__', '__delattr__', '__dir__', '__doc__', '__eq__',
'__format__', '__ge__', '__getattribute__', '__gt__', '__hash__', '__iand__', '__init__',
'__init_subclass__', '__ior__', '__isub__', '__iter__', '__ixor__', '__le__', '__len__',
'__lt__', '__ne__', '__new__', '__or__', '__rand__', '__reduce__', '__reduce_ex__',
'__repr__', '__ror__', '__rsub__', '__rxor__', '__setattr__', '__sizeof__', '__str__',
'__sub__', '__subclasshook__', '__xor__',
'add', 'clear', 'copy', 'difference', 'difference_update', 'discard', 'intersection',
'intersection_update', 'isdisjoint', 'issubset', 'issuperset', 'pop', 'remove',
'symmetric_difference', 'symmetric_difference_update', 'union', 'update']| Método | Descripción | Ejemplo |
|---|---|---|
| add | Añade un elemento al final del conjunto | set.append(5) |
| clear | Elimina toda la información del conjunto | set.clear() |
| copy | Devuelve una copia del conjunto | set.copy() |
| difference | Devuelve las diferencias entre un conjunto sobre otro | set.difference(st2) |
| difference_update | Aplica las diferencias al primer conjunto | set.difference_update(st2) |
| discard | Intenta eliminar un elemento del conjunto, exista o no | set.discard('e') |
| intersection | Devuelve un conjunto con los elementos que están en otros dos | set.intersection(st2) |
| intersection_update | Simila a intersection pero actualizando el primer conjunto con el resultado | set.intersection_update(st2) |
| isdisjoint | Devuelve True si la intersección de los conjuntos vacía | set.isdisjoint(st2) |
| issubset | Devuelve True si el otro conjunto contiene el primero | set.issubset(st2) |
| issuperset | Devuelve True si el primer conjunto contiene el segundo | |
| pop | Devuelve y elimina un elemento arbitrario o devuelve un error si está vacío | set.pop() |
| remove | Intenta eliminar un elemento del conjunto, si no existe eleva un error | set.remove(2) |
| symmetric_difference | Devuelve los elementos que están exactamente en uno de los sets | set.symmetric_difference(st2) |
| symmetric_difference_update | Similar a symmetric_difference pero actualizando el primer conjunto | set.symmetric_difference_update(st2) |
| union | Devuelve un conjunto con todos los elementos de ambos conjuntos | set.union(st2) |
| update | Actualiza el primer conjunto con otro | set.update(st2) |
Operaciones de álgebra de conjuntos en Python
A continuación se muestran ejemplos de uso del álgebra de conjuntos, para el cual usaremos el ejemplo de los estudiantes en los grupos.
>>> group_a.union(group_b)
{'Ana', 'Antonio', 'Pedro', 'Carlos', 'Marcos', 'Mario'}
>>> group_a.difference(group_b)
{'Marcos', 'Mario'}
>>> group_a.intersection(group_b)
{'Ana', 'Carlos'}
>>> group_a.isdisjoint(group_b)
False
>>> group_a.isdisjoint({1, 2})
True
>>> group_a.issubset(group_b)
False
>>> group_a.issubset({'Marcos'})
False
>>> group_a.issubset(group_a)
True
>>> group_a.issuperset(group_a)
True
>>> group_a.issuperset(group_b)
False
>>> group_a.issuperset({'Marcos'})
True
>>> group_a.symmetric_difference(group_b)
{'Antonio', 'Pedro', 'Marcos', 'Mario'}Operaciones con conjuntos
También se pueden realizar operaciones usuales sobre conjuntos como sumas, eliminaciones de elementos o comparaciones.
>>> len(group_a)
4
>>> group_a.add('Pepe')
>>> group_a
{'Ana', 'Pepe', 'Carlos', 'Marcos', 'Mario'}
>>> group_a.remove('Ana')
>>> group_a
{'Pepe', 'Carlos', 'Marcos', 'Mario'}
>>> group_a.pop()
'Pepe'
>>> group_a
{'Carlos', 'Marcos', 'Mario'}
>>> group_a.pop()
'Carlos'
>>> group_a
{'Marcos', 'Mario'}
>>> group_a.remove('Pepe')
Traceback (most recent call last):
File "<stdin>", line 1, in <module>
KeyError: 'Pepe'
>>> group_a.discard('Pepe')
>>> group_a > group_b
False
>>> group_a + group_b
Traceback (most recent call last):
File "<stdin>", line 1, in <module>
TypeError: unsupported operand type(s) for +: 'set' and 'set'
>>> group_a or group_b
{'Marcos', 'Mario'}
>>> group_a and group_b
{'Ana', 'Carlos', 'Antonio', 'Pedro'}
>>> group_a, group_b
({'Marcos', 'Mario'}, {'Ana', 'Carlos', 'Antonio', 'Pedro'})Frozenset en Python
Los conjuntos son mutables en Python, sin embargo, existe un tipo similar que son los frozenset (conjuntos congelados).
La diferencia principal con respecto a los conjuntos (set) es que son inmutables por lo que no se pueden añadir ni eliminar elementos una vez creados, pero sus características son similares.
- Contienen elementos únicos.
- Se representan en forma de vectores.
- La creación se hace usando
frozenset(argumentos). - Los elementos no se pueden alterar una vez inicializados.
- Sus elementos no están ordenados.
- Ocupan menos espacio que los conjuntos.
>>> frozenset(range(5))
frozenset({0, 1, 2, 3, 4})
>>> fs = frozenset(range(5))
>>> fs.add(9)
Traceback (most recent call last):
File "<stdin>", line 1, in <module>
AttributeError: 'frozenset' object has no attribute 'add'
>>> 2 in fs
True
>>> frozenset([1, 45, 3j, 'hola'])
frozenset({'hola', 1, 3j, 45})
>>> dir(frozenset)
['__and__', '__class__', '__contains__', '__delattr__', '__dir__', '__doc__', '__eq__', '__format__', '__ge__', '__getattribute__', '__gt__', '__hash__', '__init__', '__init_subclass__', '__iter__', '__le__', '__len__', '__lt__', '__ne__', '__new__', '__or__', '__rand__', '__reduce__', '__reduce_ex__', '__repr__', '__ror__', '__rsub__', '__rxor__', '__setattr__', '__sizeof__', '__str__', '__sub__', '__subclasshook__', '__xor__', 'copy', 'difference', 'intersection', 'isdisjoint', 'issubset', 'issuperset', 'symmetric_difference', 'union']Libros recomendados para aprender Python
Estos son los libros que pueden ayudarte a aprender Python, aprender a programar, tipos de datos, algoritmia y mucho más.